I wish to call this series ‘A paper a day keeps the doctor away’. Hope you enjoy it!
Paper
On the importance of single directions for generalization (Ari S. Morcos et al.)
ICLR 2018
Citation 68
In One Sentence
This paper shows that there is a strong negative correlation between reliance of single direction of features (measured mainly by activation of single unit) and the generalization performance across a variety of settings, including purely training randomness, corrupted labels and during the training procedures and hence cast doubts on the importance of selective neurons in the neural network.
Main Content
- Selectivity definition of a unit (a feature map for CNN or a neuron for MLP)
$selectivity = \frac{\mu_{max}-\mu_{-max}}{\mu_{max}+\mu_{-max}}$
Here $\mu_{max}$ is the highest class-condition mean activity and $\mu_{-max}$ representing the mean activity across all other classes.
In Appendix A.5, the authors argue that this definition yield similar result with mutual information.
- Selectivity and generalization
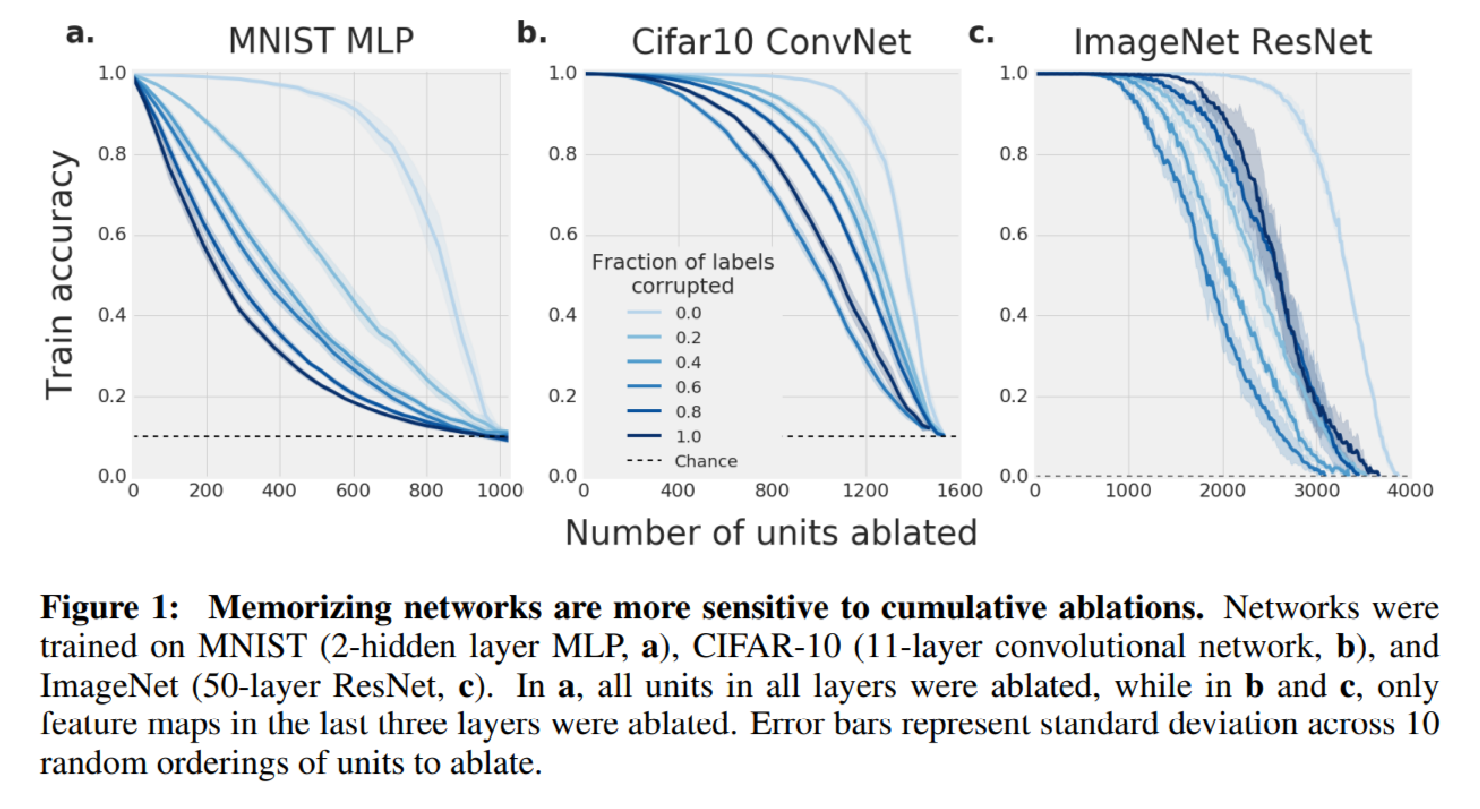
For memorizing network, it should use more of its capacity than the structure-finding network and by extension, more single directions. Hence perturbation of random single direction should interfere with the representation of the data higher.
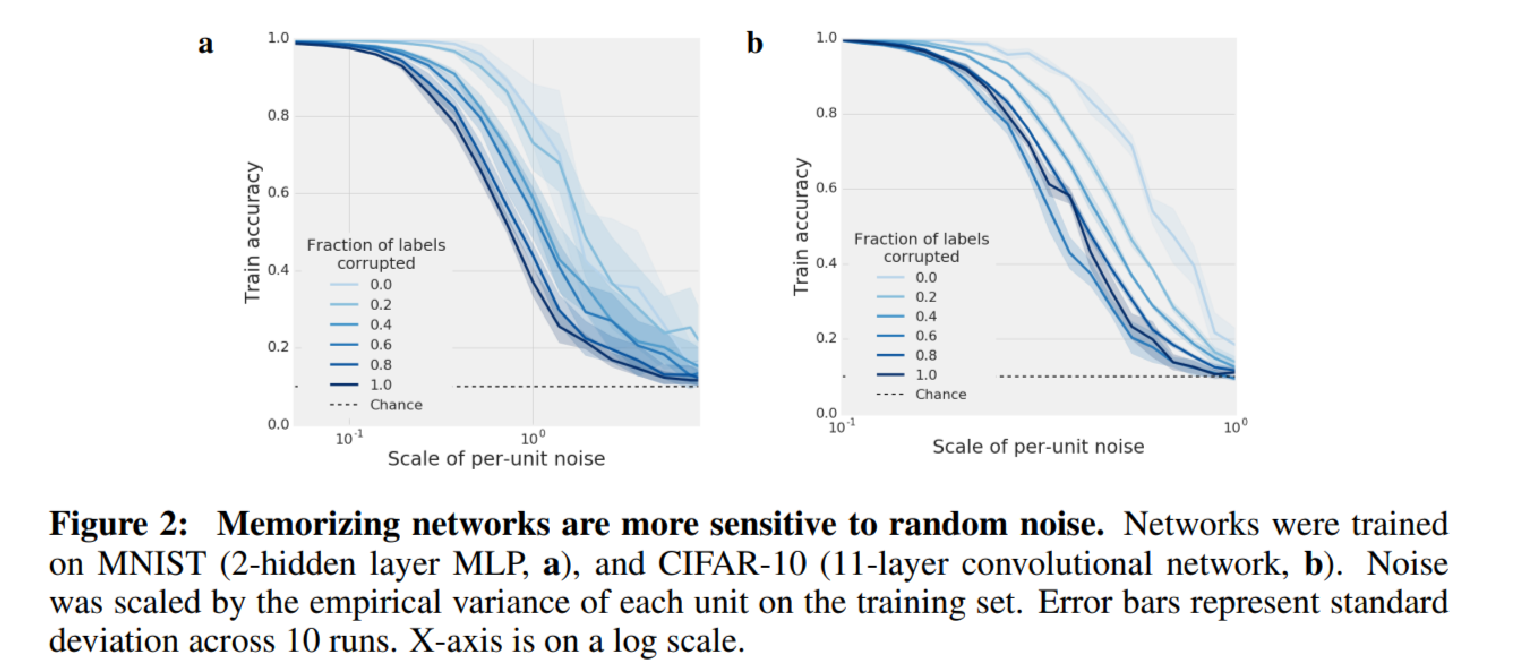
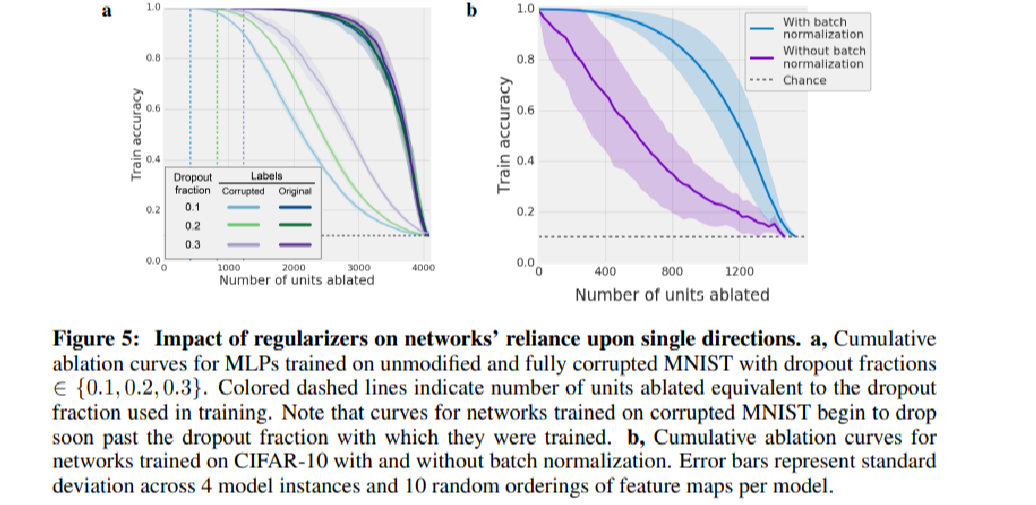
Hence the authors train a variety of networks type on datasets with differing fractions of randomized labels and evaluate their performance as progressively larger fractions of corrupted labels. Here we know intuitively as the fraction goes up, the model will generalize poorer. Consistent with this intuition, the model become more sensitive to the per unit ablation(Figure 1) and uniform normal random noise applied unit wise.
Here ablation is performed by setting the activation of the units to zero. The authors have tested two ways and discover that clamping the activation of the units to empirical mean activation on the training set was more damaging to the network’s performance.
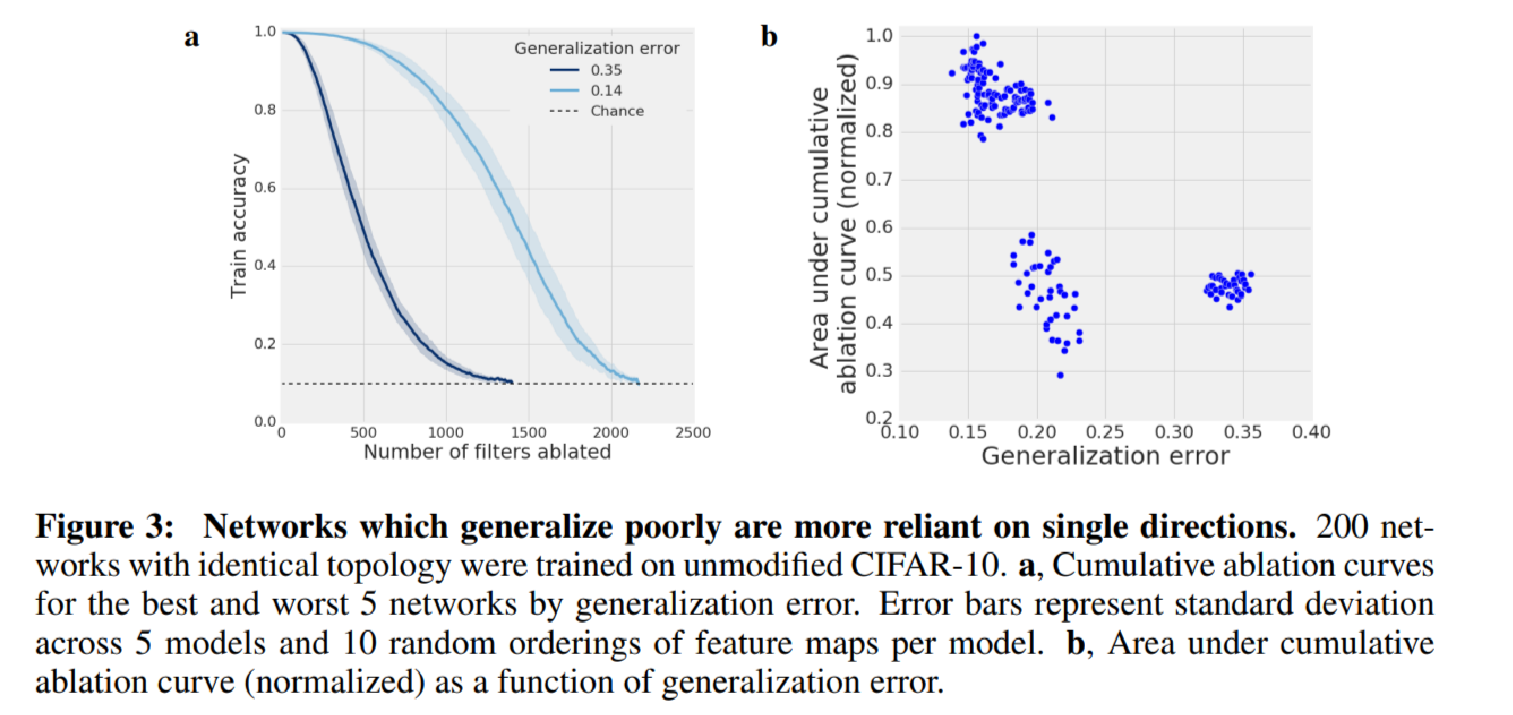
Further the authors find that there is high negative correlation of generalization error and the area under cumulative ablation curve (AUC) for networks with same topology trained with same procedure with different random seeds. The authors have suspected that the clustering in the image degeneracy caused by optimization. But this hypothesis remain untested.
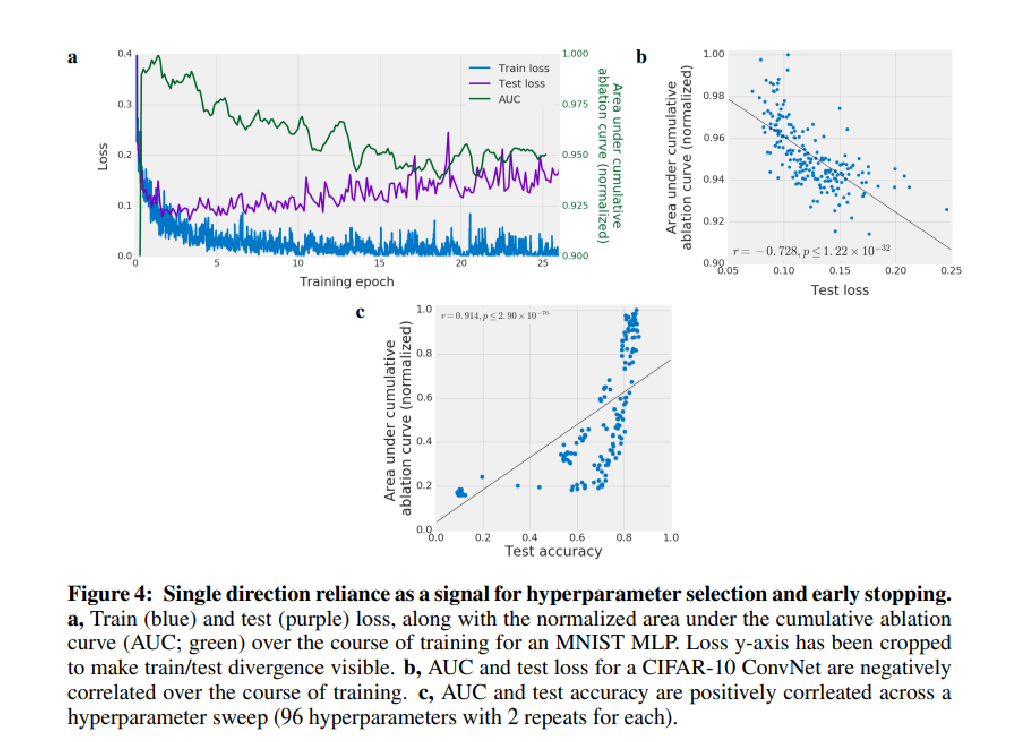
This definition can also be used to predict generalization as authors shows that generalization error is negatively correlated with AUC during training and the AUC decrease almost at the exact same time training and test loss diverges.
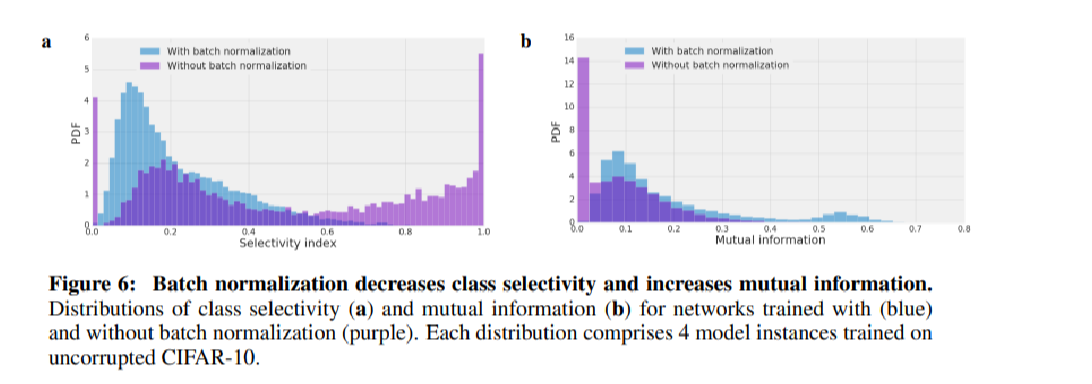
The author also tested dropout and batch normalization and their impacts on the reliance. Not surprisingly, both ways reduce the reliance but are not able to reduce it to zero. For dropout, the dependence of test accuracy number of neuron ablated has almost been exactly removed but after this threshold the trend still persists. For batch normalization, strangely, it will significantly reduce the number of high selective neurons but increase the neurons’ mutual informations.
Finally the author ask the fundamental question, does highly selective neuron really important for the output of the networks, given that we know the less reliant on single directions exhibit better generalization performance?
The author suspected from the batch normalization experiment that this may not be the case. A proof of principle experiment is conducted as the authors ablated out different units and try to find the correlation of the selectivity or mutual information of ablated units and the increment of test loss and found that the correlation is negligible.
Reflection
Definition
- On definition of selectivity
If an unit has low activation iff the input belongs to one class, selectivity may still be very low, undermining the universality of this definition.
Then an alternative interpretation of what the author have shown in the batch normalization experiment may be that the selectivity definition fails to capture information neuron stored.
Generalization Experiment
- Choice of ablation
It is not logically valid to choose the ablation value to zero only because it affect the network milder.
- The random noise experiment
To me it feels like that the random noise experiment conducted by adding noise of uniform direction and increasing variance, it is hard to see how this is link to the reliance of neural net on number of feature direction, or possibly interpreted as the dimension of manifold the data lies on at some hidden layer, which maybe highly unlinear and it is not clear what is the correct interpretation of this experiment.
Importance experiment
- Correlation experiment
It is questionable that whether ablation of one unit is too minor for a neural networks and that all the impact on the loss will hence only be out of noise, which can explain why no correlation is found. Perhaps grouping ablation will make more sense.